En este artículo
AES
AES (Advanced Encryption Standard) es uno de los algoritmos de cifrado más utilizados en todo el mundo. Su origen se remonta a finales de la década de 1990, cuando el Instituto Nacional de Estándares y Tecnología de los Estados Unidos (NIST) lanzó una convocatoria pública para encontrar un algoritmo de cifrado simétrico que reemplazara al ya obsoleto DES (Data Encryption Standard). Este proceso fue una respuesta a la creciente necesidad de fortalecer la seguridad en la transmisión de datos en un entorno digital cada vez más complejo.
Cronología del Proceso de Selección
-
1997: El NIST lanza una convocatoria para recibir propuestas de algoritmos que pudieran ser candidatos para convertirse en el nuevo estándar de cifrado.
-
Agosto de 1998: Se reciben un total de 15 propuestas de algoritmos de cifrado, de las cuales algunos provenían de destacados investigadores y criptógrafos de todo el mundo.
-
Agosto de 1999: Tras un exhaustivo proceso de evaluación y análisis, se seleccionan 5 algoritmos finalistas. Estos algoritmos fueron evaluados por su seguridad, eficiencia y rendimiento.
-
2 de octubre de 2000: Finalmente, el algoritmo denominado Rijndael fue elegido como el nuevo AES. Este algoritmo, desarrollado por los criptógrafos belgas Vincent Rijmen y Joan Daemen, se destacó por su simplicidad y robustez frente a posibles ataques criptográficos.
A la hora de cifrar datos, AES los divide en bloques de 128 bits (16 bytes) y los cifra a través de varias rondas. Cada bloque de 16 bytes se denomina “estado”. El número de rondas varía según la longitud de la clave utilizada en el algoritmo:
AES 128 -> 10 rondas
AES 192 -> 12 rondas
AES 256 -> 14 rondas
En AES se pueden diferenciar 4 fases:
- SubByte
- ShiftRows
- MixColumns
- AddRoundKey
El algoritmo comienza con la fase AddRoundKey utilizando la clave de cifrado sin alterar.
Después, para todas las rondas excepto la última, realizará las 4 etapas que hemos visto anteriormente.
Mientras que para la última ronda, pasará por todas las fases excepto por la de MixColumns.
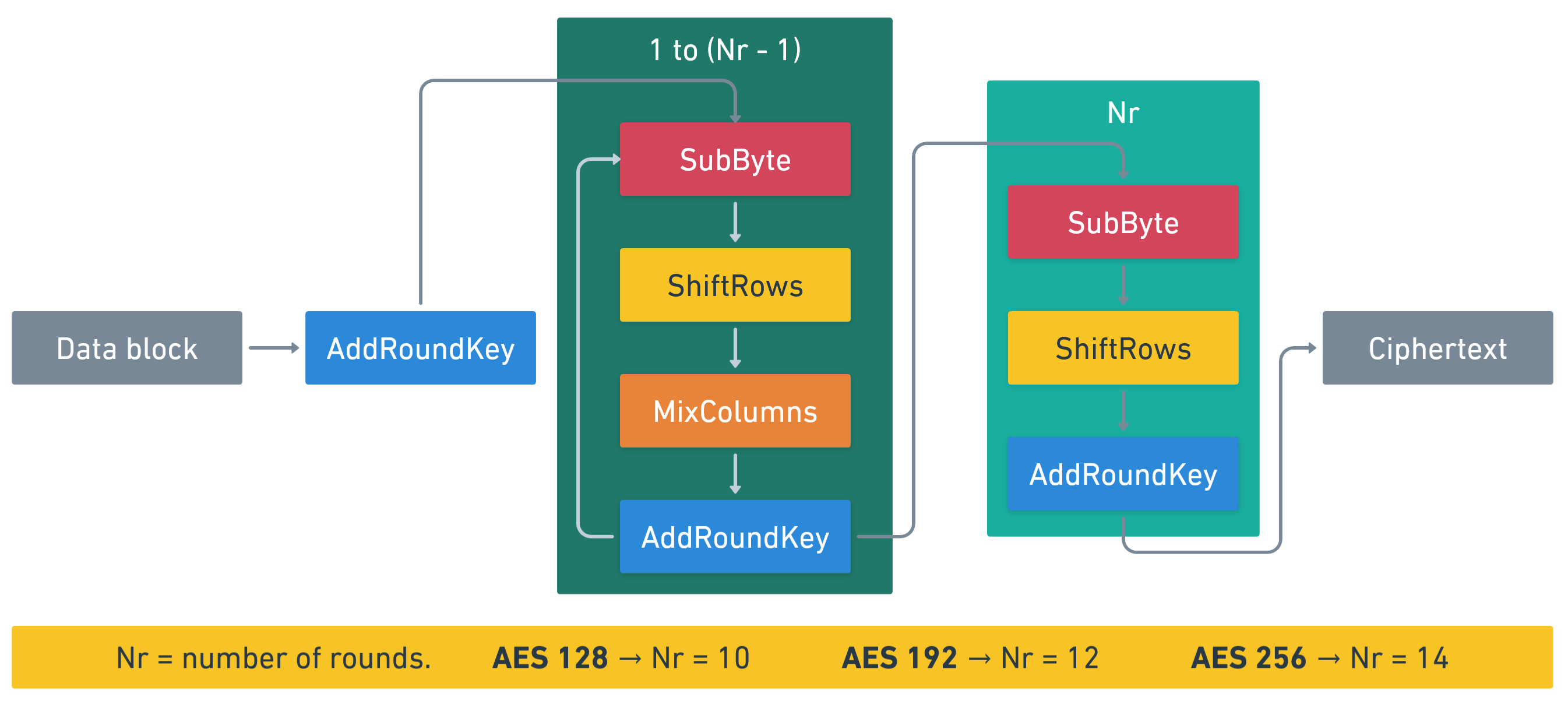
Veamos en más profundidad en qué consisten estas fases.
1. SubByte
Esta estapa introduce confusión al proceso de cifrado. En ella se realizan las sustituciones de bytes utilizando la tabla S-box. Esta tabla es una matriz preestablecida de sustitución de 256 valores, donde cada valor posible (si lo representamos en hexadecimal serían los valores que van desde 00 a FF) tiene una correspondencia con un byte de esa tabla. Veámoslo con un ejemplo.
Tenemos el valor hexadecimal:
Ai = f5
Si vemos la imagen de abajo podemos apreciar que la ‘x’ representa las filas de la tabla S-box, mientras que la ‘y’ representa las columnas.
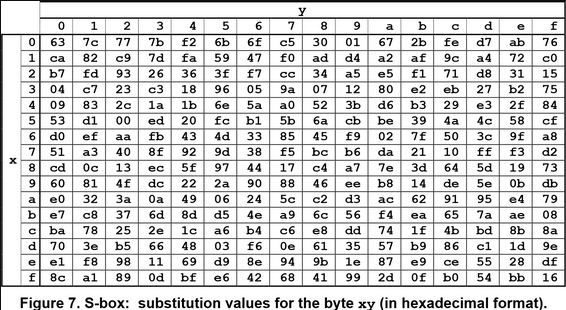Fuente: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf
Siguiendo esa regla:
x = f
y = 5
Si la ‘x = f’ entonces obtendremos un valor de la última fila, la de la letra ‘f’. Y si ‘y = 5’, nuestro valor sustituido estará en la fila ‘f’ columna ‘5’ es decir, ‘e6’ que representaremos como ‘Bi’.
Ai = f5 -> S-box -> e6 = Bi
Cálculo de la tabla S-box
Pero, ¿cómo se calculan los valores de esta tabla? Para obtener cada valor:
- Se calcula el inverso multiplicativo en GF(2^8).
- Se aplica una función afín.
GF(2^8) es el campo de Galois que tiene 256 elementos (2^8 = 256). Una definición muy superficial de ‘campo’ puede ser esta: conjunto de elementos dónde se puede sumar, restar, multiplicar y dividir (dónde todos los elementos excepto 0 tienen inverso multiplicativo). En GF(2^8), cada elemento es un polinomio de, como máximo, grado 7 (x^7) y los campos de Galois de base 2 (GF(2)) solo puede tener como coeficientes 0 o 1. Creo que con un ejemplo lo veremos mejor.
Volvamos a nuestro byte hexadecimal:
Ai = f5
La representación binaria de ‘f5’ sería:
f = 1111
5 = 0101
Es decir:
Ai = 1111 0101
Aunque no lo parezca, porque hemos dicho que los elementos de GF(2^8) son polinomios, este número es un elemento dentro del campo GF(2^8):
Ai = 1111 0101 = 1x^7 + 1x^6 + 1x^5 + 1x^4 + 0x^3 + 1x^2 + 0x + 1 = x^7 + x^6 + x^5 + x^4 + x^2 + 1
Bits = 1 1 1 1 0 1 0 1
^ ^ ^ ^ ^ ^ ^ ^
Potencias = 7 6 5 4 3 2 1 0
Ai(x) = x^7 + x^6 + x^5 + x^4 + x^2 + 1
Podría decirse, de forma intuitiva, que cada potencia representa la posición de un bit dentro de un byte (8 bits).
Cálculo del inverso multiplicativo
Entendido esto, podemos pasar a ver qué es el inverso de un número. Dado un número ‘a’ su inverso ‘a^(-1)’ será aquel que multiplicado por ‘a’ nos devuelva el resultado ‘1’:
a · a^(-1) = 1
Queremos obtener el inverso de Ai(x):
Ai(x) · Ai(x)^(-1) = 1.
El valor de Ai(x)^(-1), si ‘Ai(x) = x^7 + x^6 + x^5 + x^4 + x^2 + 1’ es:
Polinomio: x^6 + x^2 + x
Bits: 0100 0110
Hexadecimal: 46
Por aquí dejo todos los inversos multiplicativos para cada valor posible:
| 0 1 2 3 4 5 6 7 8 9 a b c d e f
--|--|--|--|--|--|--|--|--|--|--|--|--|--|--|--|--|
0 |-- 01 8d f6 cb 52 7b d1 e8 4f 29 c0 b0 e1 e5 c7
1 |74 b4 aa 4b 99 2b 60 5f 58 3f fd cc ff 40 ee b2
2 |3a 6e 5a f1 55 4d a8 c9 c1 0a 98 15 30 44 a2 c2
3 |2c 45 92 6c f3 39 66 42 f2 35 20 6f 77 bb 59 19
4 |1d fe 37 67 2d 31 f5 69 a7 64 ab 13 54 25 e9 09
5 |ed 5c 05 ca 4c 24 87 bf 18 3e 22 f0 51 ec 61 17
6 |16 5e af d3 49 a6 36 43 f4 47 91 df 33 93 21 3b
7 |79 b7 97 85 10 b5 ba 3c b6 70 d0 06 a1 fa 81 82
8 |83 7e 7f 80 96 73 be 56 9b 9e 95 d9 f7 02 b9 a4
9 |de 6a 32 6d d8 8a 84 72 2a 14 9f 88 f9 dc 89 9a
a |fb 7c 2e c3 8f b8 65 48 26 c8 12 4a ce e7 d2 62
b |0c e0 1f ef 11 75 78 71 a5 8e 76 3d bd bc 86 57
c |0b 28 2f a3 da d4 e4 0f a9 27 53 04 1b fc ac e6
d |7a 07 ae 63 c5 db e2 ea 94 8b c4 d5 9d f8 90 6b
e |b1 0d d6 eb c6 0e cf ad 08 4e d7 e3 5d 50 1e b3
f |5b 23 38 34 68 46 03 8c dd 9c 7d a0 cd 1a 41 1c
Fuente: https://samiam.org/galois.html
Aplicación de la función afín
Una vez calculado el inverso, hay que aplicar una función afín para romper la linealidad. Este proceso se compone de la multiplicación de una matriz fija 8x8 (M) por la representación en bits del inverso recién calculado (Ai(x)^(-1)) seguido de una suma de un byte constante (C):
Bi = M · Ai^(-1) + C
[ 1 1 1 1 1 0 0 0 ] [ 0 ] [ 0 ]
[ 0 1 1 1 1 1 0 0 ] [ 1 ] [ 1 ]
[ 0 0 1 1 1 1 1 0 ] [ 0 ] [ 1 ]
Bi = [ 0 0 0 1 1 1 1 1 ] · [ 0 ] + [ 0 ]
[ 1 0 0 0 1 1 1 1 ] [ 0 ] [ 0 ]
[ 1 1 0 0 0 1 1 1 ] [ 1 ] [ 0 ]
[ 1 1 1 0 0 0 1 1 ] [ 1 ] [ 1 ]
[ 1 1 1 1 0 0 0 1 ] [ 0 ] [ 1 ]
Fuente: https://www.redalyc.org/journal/5122/512253718012/html/
Tenemos que explicar que en GF(2^8) las sumas se realizan como una función XOR, donde si se comparan dos valores, el resultado será verdadero sólo si uno de ellos es verdadero y el otro falso.
Al hablar de bits el ‘0’ representará el valor falso (False), mientras que el ‘1’ representará verdadero (True):
AND | OR | XOR
-----------------------------------
1 + 1 = 1 | 1 + 1 = 1 | 1 + 1 = 0
1 + 0 = 0 | 1 + 0 = 1 | 1 + 0 = 1
0 + 1 = 0 | 0 + 1 = 1 | 0 + 1 = 1
0 + 0 = 0 | 0 + 0 = 0 | 0 + 0 = 0
Es decir, si el byte que resulta después de la multiplicación M · Ai(x)^(-1) (al que llamaremos ‘z’) lo sumamos a C obtendremos:
Bi = M · Ai^(-1) + C
z = M · Ai^(-1)
Bi = z + C
z | C | z + C | Bi
-----------------------------------
[ 1 ] [ 0 ] | [ 1 + 0 ] = [ 1 ]
[ 0 ] [ 1 ] | [ 0 + 1 ] = [ 1 ]
[ 0 ] [ 1 ] | [ 0 + 1 ] = [ 1 ]
[ 0 ] + [ 0 ] | [ 0 + 0 ] = [ 0 ]
[ 0 ] [ 0 ] | [ 0 + 0 ] = [ 0 ]
[ 1 ] [ 0 ] | [ 1 + 0 ] = [ 1 ]
[ 0 ] [ 1 ] | [ 0 + 1 ] = [ 1 ]
[ 1 ] [ 1 ] | [ 1 + 1 ] = [ 0 ]
Bi = 1110 0110 = e6
Así es como se obtienen los valores de la S-box.
2. ShiftRows
Esta operación es muy sencilla, simplemente se rotan los bytes de cada fila del estado (nuestra matriz de 16 bytes) un cierto número de posiciones a la izquierda. Esta fase junto con la siguiente (MixColumns) aportan difusión al algoritmo.
Antes Después
[ b0 b4 b8 b12 ] -> Fila 0: no cambia -> [ b0 b4 b8 b12 ]
[ b1 b5 b9 b13 ] -> Fila 1: rota 1 byte -> [ b5 b9 b13 b1 ]
[ b2 b6 b10 b14 ] -> Fila 2: rota 2 bytes -> [ b10 b14 b2 b6 ]
[ b3 b7 b11 b15 ] -> Fila 3: rota 3 bytes -> [ b15 b3 b7 b11 ]
3. MixColumns
En esta estapa se multiplica la matriz fija que se muestra a continuación, por cada columna del estado:
[ 02 03 01 01 ] -> Fila 0
[ 01 02 03 01 ] -> Fila 1 = Fila 0 rotada una posición hacia la derecha
[ 01 01 02 03 ] -> Fila 2 = Fila 0 rotada dos posiciones hacia la derecha
[ 03 01 01 02 ] -> Fila 3 = Fila 0 rotada tres posiciones hacia la derecha
Donde 01, 02 y 03 son valores en GF(2^8):
01 = 0000 0001 -> 1
02 = 0000 0010 -> x
03 = 0000 0011 -> x + 1
Por ejemplo, para la primera columna del estado sería:
[ c0 ] [ 02 03 01 01 ] [ b0 ]
[ c1 ] = [ 01 02 03 01 ] · [ b5 ]
[ c2 ] [ 01 01 02 03 ] [ b10 ]
[ c3 ] [ 03 01 01 02 ] [ b15 ]
c0 = 02·b0 + 03·b5 + 01·b10 + 01·b15
c1 = 01·b0 + 02·b5 + 03·b10 + 01·b15
c2 = 01·b0 + 01·b5 + 02·b10 + 03·b15
c3 = 03·b0 + 01·b5 + 01·b10 + 02·b15
Si multiplicamos todas las columnas del estado obtendremos una nueva matriz:
[ c0 c4 c8 c12 ]
[ c1 c5 c9 c13 ]
[ c2 c6 c10 c14 ]
[ c3 c7 c11 c15 ]
4. AddRoundKey
Se realiza una operación XOR entre el estado y una subclave específica para esa ronda. Esta es la única parte del algoritmo que involucra directamente la clave. Las subclaves se generan previamente mediante el proceso de expansión de clave. Veamos como sería esta fase para el texto ‘Texto de ejemplo’:
texto = 'Texto de ejemplo'
texto en hexadecimal = 546578746f20646520656a656d706c6f
Clave original de 128 bits = 2b7e151628aed2a6abf7158809cf4f3c
[ 54 ] XOR [ 2b ] = [ 7f ]
[ 65 ] XOR [ 7e ] = [ 1b ]
[ 78 ] XOR [ 15 ] = [ 6d ]
[ 74 ] XOR [ 16 ] = [ 62 ]
[ 6f ] XOR [ 28 ] = [ 47 ]
[ 20 ] XOR [ ae ] = [ 8e ]
[ 64 ] XOR [ d2 ] = [ b6 ]
[ 65 ] XOR [ a6 ] = [ c3 ]
[ 20 ] XOR [ ab ] = [ 8b ]
[ 65 ] XOR [ f7 ] = [ 92 ]
[ 6a ] XOR [ 15 ] = [ 7f ]
[ 65 ] XOR [ 88 ] = [ ed ]
[ 6d ] XOR [ 09 ] = [ 64 ]
[ 70 ] XOR [ cf ] = [ bf ]
[ 6c ] XOR [ 4f ] = [ 23 ]
[ 6f ] XOR [ 3c ] = [ 53 ]
resultado = 7f1b6d62478eb6c38b927fed64bf2353
‘7f1b6d62478eb6c38b927fed64bf2353’ serán los bytes que pasarán a la fase de SubByte (si nos encontrasemos en la última ronda, estos bytes serían el texto completamente cifrado). En este caso, al mezclar el texto plano con la clave original, nos encontramos en la ronda inicial, por lo que la siguiente estapa será SubByte.
Pero, si nos encontrasemos en cualquier ronda que no fuese la inicial, ¿qué claves estaríamos utilizando?. Para el resto de rondas se utilizarán subclaves derivadas de la clave original, y la forma de calcularlas la vamos a ver a continuación.
Expansión de clave
En este proceso se crean ‘Nr+1’ subclaves que se utilizarán en la fase de AddRoundKey, donde ‘Nr’ es el número de rondas dependiendo del tamaño de la clave de AES:
AES 128 -> 10 rondas -> 11 subclaves
AES 192 -> 12 rondas -> 13 subclaves
AES 256 -> 14 rondas -> 15 subclaves
¿Cuáles son los pasos que realiza este proceso? Veámoslo para AES 128.
Primero divide la clave original en palabras de 32 bits, 4 palabras en total. Por ejemplo:
Clave original de 128 bits = 2b7e151628aed2a6abf7158809cf4f3c
División en palabras de 32 bits:
w0 = 2b7e1516
w1 = 28aed2a6
w2 = abf71588
w3 = 09cf4f3c
Si queremos obtener la siguiente subclave necesitaremos calcular 4 palabras más: w4, w5, w6, w7 (128 bits en total).
Dependiendo del índice que tenga esa palabra se llevarán a cabo unas operaciones u otras.
El índice es multiplo de 4
Si el índice es múltiplo de 4, ‘i % 4 = 0’ (en nuestro ejemplo solo el índice 4 lo es) se realizarán estas operaciones:
-
RotWord: rota los 4 bytes de la palabra w[i-1] un byte a la izquierda. En nuestro ejemplo:
i = 4 w[i-1] = w[4 - 1] = w[3] = 09cf4f3c 09cf4f3c -> RotWord -> cf4f3c09De momento w4 es w3 con sus bytes rotados una posición a la izquierda.
-
SubWord: aplica la S-Box a cada byte de ese resultado:
cf 4f 3c 09 -> Sbox -> 8a 84 eb 01 -
XOR con Rcon: XOR del resultado anterior con el valor constante Rcon[i/4]. En este caso, tenemos que aclarar todos los valores posibles para Rcon:
Valores en hexadecimal de Rcon por cada ronda en AES 128: Ronda 0 -> 00000000 Ronda 1 -> 01000000 Ronda 2 -> 02000000 Ronda 3 -> 04000000 Ronda 4 -> 08000000 Ronda 5 -> 10000000 Ronda 6 -> 20000000 Ronda 7 -> 40000000 Ronda 8 -> 80000000 Ronda 9 -> 1B000000 Ronda 10 -> 36000000Como podemos ver, la única parte que puede afectar a la palabra que pretendemos calcular es el primer byte, porque el resto son ceros. Entonces solo se alterará el primer byte de nuestra palabra. Continuemos con nuestro ejemplo:
i = 4 Rcon[i/4] = Rcon[4/4] = Rcon[1] Rcon[1] = 01000000 [ 8a ] XOR [ 01 ] = [ 8b ] [ 84 ] XOR [ 00 ] = [ 84 ] [ eb ] XOR [ 00 ] = [ eb ] [ 01 ] XOR [ 00 ] = [ 01 ] -
XOR con w[i-4]: XOR de la palabra w[i-4] con el resultado anterior:
i = 4 w[i-4] = w[4-4] = w[0] = 2b7e1516 w[i] = w[i-4] XOR w[i]' [ 2b ] XOR [ 8b ] = [ a0 ] w[0] XOR w[4] = [ 7e ] XOR [ 84 ] = [ fa ] [ 15 ] XOR [ eb ] = [ 9e ] [ 16 ] XOR [ 01 ] = [ 17 ] w[4] = a0fa9e17
Después de estas cuatro fases habremos calculado la palabra w4: a0fa9e17
El indice no es múltiplo de 4
Cuando el índice no es múltiplo de 4 ‘i % 4 != 0’ (en nuestro ejemplo, todos los índices excepto 4), solo hace el XOR con la palabra w[i-4]:
i = 5
w[i] = w[i-4] XOR w[i-1]
w[5] = w[5-4] XOR w[5-1] = w[1] XOR w[4]
[ 28 ] XOR [ a0 ] = [ 88 ]
w[1] XOR w[4] = [ ae ] XOR [ fa ] = [ 54 ]
[ d2 ] XOR [ 9e ] = [ 4c ]
[ a6 ] XOR [ 17 ] = [ b1 ]
w[5] = 88544cb1
De esta forma, podemos calcular también w6 y w7 para obtener la subclave completa para la ronda 1. Para el resto de rondas, seguirá el mismo proceso. Como hemos dicho anteriormente, para la ronda inicial la “subclave” que se utilizará será la clave original.
A fecha de este artículo, no se ha encontrado ninguna vulnerabilidad práctica que permita romper la seguridad de este algoritmo. Por esa razón, AES se ha consolidado como el estándar de cifrado más utilizado a nivel mundial, gracias a su robustez y eficiencia en la protección de datos sensibles, sin sacrificar el rendimiento.
A medida que la tecnología avanza y las técnicas de ataque se vuelven más sofisticadas, la importancia de utilizar algoritmos de cifrado confiables como AES se vuelve aún más crítica. La adopción generalizada de este estándar en aplicaciones que van desde la banca en línea hasta la comunicación segura, pone de manifiesto su relevancia en el mundo digital actual.
En un entorno donde la privacidad y la seguridad son primordiales, AES no solo representa una solución técnica, sino también un pilar fundamental en la confianza que los usuarios depositan en las tecnologías de la información.